free to write WHATEVER I like

　《過去の戦歴》
　センター試験数学ⅠA（2012年度分）を約12年ぶりに解いてみた（旧ブログ）
　【数学ⅠA】2013年センター試験を昨年に続いて解いてみた
　【数学ⅠA】2014年センター試験を3年連続で解いてみた
　【数学ⅠA】センター試験（2015年）を解いてみた（4年連続）
　【数学ⅠA】センター試験（2016年）を解いてみた（5年連続）

　＜予備校による解説＞
　東進ハイスクール　センター試験2017年　数学ⅠA

　30歳を過ぎてからなぜか毎年この時期にセンター試験の数学の問題を解くようになり、今年で6年目である。今年の数学ⅠAは1問間違えて、1問はどうしても解けなかった（悔しい）。整数の問題は相変わらず苦手である。下記の画像でもお解りのように、力技でかなり強引に解いた。以下の難易度は、あくまでも私の主観である。

　【第1問】《難易度：★★☆》式の計算／命題と条件／2次関数
　〔1〕は単純な式の計算。〔2〕の「命題と条件」で1問間違えてしまった。（pまたはqの否定）（x＝1またはx²≠1）⇒q（x²＝1）は偽である（反例：x＝1）。また、q（x²＝1）⇒（pまたはqの否定）（x＝1またはx²≠1）も偽である（反例：x＝－1）。よって、（pまたはqの否定）はqであるための「必要条件でも十分条件でもない」が正解。〔3〕の「2次関数」も単純な計算問題。最後に頂点のy座標の最小値を求めるところで、下図ではいきなりt＝0のとき最小値となると書いてしまったが、正確には、t＝a²よりt≧0であるから、t＝0のとき最小値となる、と書くのが正しい。

　【第2問】《難易度：★☆☆》三角比／データと分析
　〔1〕は正弦定理、余弦定理、三角比を用いた三角形の面積の求め方を知っていれば解ける。△ABCの外接円の半径を求めるところで、下図では正弦定理を用いてAC/sin∠ABC＝2Rと書いているが、右辺は「直径の2倍」だと勘違いしたまま、さらに求めるのも外接円の「直径」だと勘違いしたまま解いていた（汗）。結果的に正解だったからよかったが・・・。〔2〕の「データ分析」は、私が高校生の時には学習範囲外だったため省略。ただ、基本的な統計の問題であり、中小企業診断士の試験にも出てくるような問題であるから、来年は解けるようになりたい。

　【第3問】《難易度：★★☆》確率
　和事象を尋ねる問題が目新しいと感じた。B、Cの少なくとも一方があたりくじを引く場合は、「Bのみがあたりを引く（P）」、「Cのみがあたりを引く（Q）」、「AとBがあたりを引く（R）」、「BとCがあたりを引く（S）」、「CとAがあたりを引く（T）」の5つの場合である。

　⓪Aがはずれのくじを引く事象⇒BまたはCがあたりを引く事象
　①Aだけがはずれのくじを引く事象⇒BとCがあたりを引く事象
　②Bがはずれのくじを引く事象⇒CまたはAがあたりを引く事象
　③Bだけがはずれのくじを引く事象⇒CとAがあたりを引く事象
　④Cがはずれのくじを引く事象⇒AまたはBがあたりを引く事象
　⑤Cだけがはずれのくじを引く事象⇒AとBがあたりを引く事象

　P、Q、Sを合わせたものが①に該当する。Rは⑤に、Tは③に該当する。よって、事象E₂は①③⑤の和事象である。くじ引きの対象性より、B、Cの少なくとも一方があたりのくじを引く確率、C、Aの少なくとも一方があたりのくじを引く確率、A、Bの少なくとも一方があたりのくじを引く確率は等しい。これに気づけば、（5）は3つの条件つき確率を計算しなくても回答できる。

　【第4問】《難易度：★★★》実数
　（2）は力技で説いた。7b5cが4でも9でも割り切れる時、7b5cは36の倍数である。7b5c＝7000＋100b＋50＋c＝36（195＋2b）＋（28b＋c＋30）と変形し、（28b＋c＋30）が36の倍数となるようなb、cの組み合わせを、実際にb、cをそれぞれ0～9まで変化させて発見した。ただし、cに関して言えば、7b5cが36の倍数であることから、cは0、2、4、6、8のいずれかでしかないので、多少は絞り込める。本当の解き方は次の通りである。まず、7b5cが4で割り切れることから、5cが4の倍数であるため、cは2または6に限定される。次に、7b5cが9で割り切れることから、各位の数の和は9の倍数であり、7＋b＋5＋c＝12＋b＋cは9の倍数である。0≦b＋c≦18より、12≦12＋b＋c≦30であり、b＋c≦18となる。c＝2の時、b＝4、c＝6の時、b＝0、9となる。

　1188の全ての正の約数の積を2進数で表す時、2＝10_（2）であるから、2の倍数を1つかけるたびに0が1つ増えることが解る。4＝100_（2）より、4の倍数を1つかけると0が2つ増えることに注意すると、求める0の数は、2の倍数の数と4の倍数の和である。

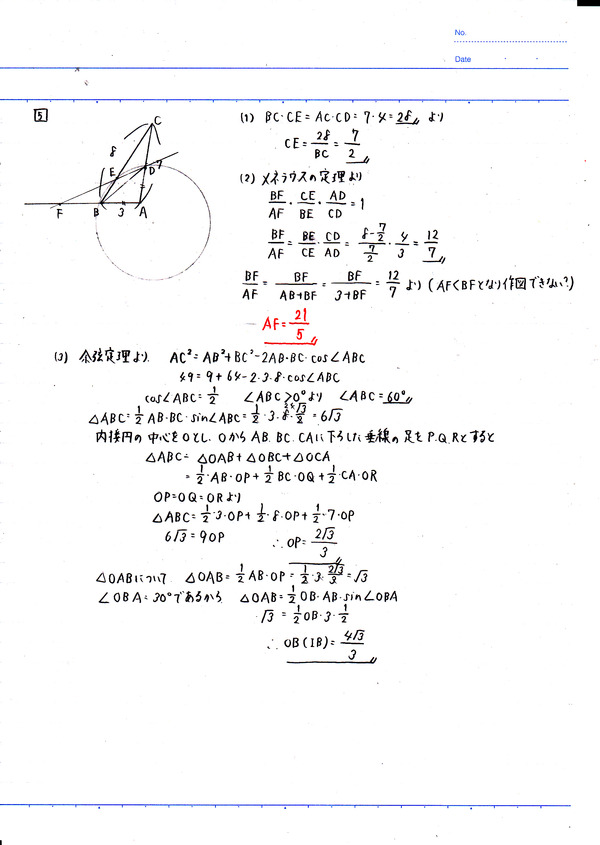
　【第5問】《難易度：★★☆》平面図形／三角比
　私の作図がそもそも間違っていた（大汗）。△ABDの内接円と書かれているのに、BとDしか通っていない。BC・CEは直感的にAC・ADに等しいだろうと思って計算した。正確に作図すれば、方べきの定理を用いることになる。私の作図ではAF＞BFとなるが、メネラウスの定理を使ってBF/AFを計算したところ12/7となった。これはBF＞AFを意味しており、図が矛盾してここで詰んだ。正確に作図していればちゃんとBF＞AFとなるため、BF/AF＝12/7よりAFが計算できる。

＜カテゴリ「センター試験・検定試験など」の最新記事＞

＜カテゴリ「数学」の最新記事＞

新課程チャート式基礎からの数学1+A チャート研究所 数研出版 2012-02-14 Amazonで詳しく見る by G-Tools

　今年もセンター試験の数学ⅠA・ⅡBを解いてみた。ⅡBが難しかったとネット上で受験生が悲鳴を上げていたようだが、IAもやや難化した印象を受けた（厳密に言えば、難しいというよりも、計算がひたすら面倒くさい感じだった）。

　なお、今年から新しい学習指導要領に対応しているようで、第3問が「データの分析」という問題であった。ただ、私が高校生だった時代にはこの分野は学習していないので、第3問はスキップし、代わりに選択問題である第4問と第5問を両方とも解答することにした。「データの分析」はビジネスで求められる統計学の問題であり、本来ならば習っていなくても解けるのが望ましいのだが、それができなくて恥ずかしい・・・。統計学を勉強したら、第3問も追記する予定である。

　以下、私のノートを公開する。力づくで解いたり、通常とは異なる方法を使ったりしている箇所があるため、ちゃんとした解説を知りたい方は予備校のHPをご覧いただきたい。★は個人的に感じた難易度である（★易～★★★難）。

　《過去3年の戦歴》
　センター試験数学ⅠA（2012年度分）を約12年ぶりに解いてみた（※旧ブログ）
　【数学ⅠA】2013年センター試験を昨年に続いて解いてみた
　【数学ⅠA】2014年センター試験を3年連続で解いてみた

　《2015年センター試験　問題・解答》
　2015年センター試験　数学ⅠA　問題
　2015年センター試験　数学ⅠA　解答（※東進ハイスクールのHPにジャンプします）

　【第1問（2次関数：★）】
　定義域が固定されていて、軸が動く場合の最大値と最小値を考える問題。pの範囲を求める際に、等号が含まれるかどうか慎重な判断が必要である。p＝1の場合は、x＝2＝1＋pの時、最大値f（2）＝f（1＋p）、p＝2の場合は、x＝3＝1＋pの時、最小値f（3）＝f（1＋p）となる。



　【第2問（集合と命題、三角比：★★）】
　〔1〕（2）は30以下の素数を1つずつ調べれば何とかなる。
　〔2〕は正弦定理と余弦定理を駆使する。



　【第4問（場合の数：★）】
　今年の数学ⅠA、ⅡBを通じて、この設問が最も簡単だと感じた。特定のマスの色を固定すれば他のマスの色が自ずと決まるため、漏れなく数え上げればそれほど苦労せずに解ける。



　【第5問（整数の性質：★★）】
　一見すると問題文が非常に複雑に思えるが、実は単純なことを尋ねている。√amが11で割ると1余るということは、（2）より√am＝126kであり、（3）で126kを11で割ると1余るkを求めているから、「√amが11で割ると1余る⇒126kを11で割ると1余る」である。なお、（3）は、問題文からkの値が1桁であることが解るため、1～9まで順番に調べるという荒業で解を導き出した。



　【第6問（図形の性質：★★）】
　作図がきれいにできるように、今年はコンパスを購入した。最初、三角形ABDの外接円と、辺BCの点Bの側の延長線上との交点Eがなかなか作図できなくて困った。私は昔から平面幾何の問題が苦手で、邪道だが途中でベクトルを使ってしまった（多分、本当はチェバの定理などを使うのだと思う）。問題文に「∠CAB＝∠CED」とさらっと書いてあるが、これは、弧DBの円周角について∠DAB＝∠DEBが成立するためである。

＜カテゴリ「センター試験・検定試験など」の最新記事＞

＜カテゴリ「数学」の最新記事＞

新課程チャート式基礎からの数学1+A チャート研究所 数研出版 2012-02-14 Amazonで詳しく見る by G-Tools

　勝手に最近の冬の恒例行事にしている「センター試験の数学を解いてみた」も今年で3回目。今年はビシッと100点を獲得。もっとも、ノートをまとめるのに2時間かかっているので意味がないが・・・。以下、解いてみた感想。

　【第1問　［1］式と計算、［2］集合】［1］はルートに気をつけてひたすら計算するだけ。［2］はどの集合も個数がそれほど多くないので、書き出してみるのがベスト。（3）の否定を含む集合は、ド・モルガンの定理を使うのがポイントである。

　【第2問　2次関数】非常に基本的な問題。最後にある「2次関数のグラフGが x 軸と共有点を持ち、さらにその全ての共有点の x 座標が－1より大きくなるような a の値の範囲」を求めるには、Gの方程式の右辺をf（x）とおき、2次方程式f（x）＝0がx＞－1の範囲で実数解を持つための条件を求めればよい。すなわち、ⅰ）判別式≧0、ⅱ）軸の方程式＞－1、ⅲ）f（－1）＞0となる。

　【第3問　三角関数】昨年は多くの受験生を泣かせた三角関数の問題だが、今年はやや易化。と言っても、計算が面倒くさいことに変わりはない。（1）でBEを求めるところは、他に方法が思いつかず、2倍角の公式を使ってしまった（反則）。（3）は設問の「角度に注目すると」がヒントで、円周角の定理を使うといろんなことが明らかになる。

　【第4問　場合の数】いわゆる経路図の問題。指定された到達地点にたどり着くまでに、1～6の矢印をそれぞれいくつずつ使えばよいのかを考える。（4）はセンター試験なので設問による誘導があるが、これが国立大学の2次試験ならば、いきなり「交差点Aを出発し、6回移動して交差点Dにいる移動の仕方は何通りか求めよ」となるのだろう。

　《過去2年の成績》
　センター試験数学ⅠA（2012年度分）を約12年ぶりに解いてみた（※旧ブログ）
　【数学ⅠA】2013年センター試験を昨年に続いて解いてみた

　《2014年センター試験　問題・解答》
　2014年センター試験　数学ⅠA　問題
　2014年センター試験　数学ⅠA　解答（※東進ハイスクールのHPにジャンプします）

＜カテゴリ「センター試験・検定試験など」の最新記事＞

＜カテゴリ「数学」の最新記事＞